Chapter 3 Simple Linear Regression
3.1 Simple Linear Regression in the Bayesian Framework
You can watch this video as primer.
We will now add one covariate/explanatory variable to the model. Refer to Statistical Rethinking “4.4 Linear prediction” or “4.4 Adding a predictor” as it’s called in the online version of the book.
So far, our “regression” did not do much to be honest. The mean of a list of values was already calculated in the descriptive statistics section before and we have mentioned how great this statistic is as measure of location and where its weaknesses are.
Now, we want to model how body height and weight are related. Formally, one wants to predict body heights from body weights.
Here and in the Frequentist framework, we will see that it is not the same problem (and therefore results in a different statistical model) to predict body weights from body heights or vice versa.
We remember the following:
- Regress \(Y\) on \(X\), which is equivalent to predict \(Y\) from \(X\). We know X and want to predict Y.
- Regress \(X\) on \(Y\), which is equivalent to predict \(X\) from \(Y\). We know Y and want to predict X.
The word “predictor” is important here. It is a technical term and describes a variable that we know (in our case weight) and with which we want to “guess as good as possible” the value of the dependent variable (in our case height). “As good as possible” means that we put a penalty on an error. The farer our prediction is away from the true value (\(y_i\)), the higher the penalty. And not only that, but if you are twice as far away from the true value, you should be penalized four times as much. This is the idea behind the squared error loss function and the core of the least squares method. What if we would punish differently, you ask? There are many loss functions one could use (for instance the Huber loss), maybe we will see some later. For now, we punish quadratically.
We always visualize the data first to improve our understanding. First comes descriptive statistics, then one can think about modeling.
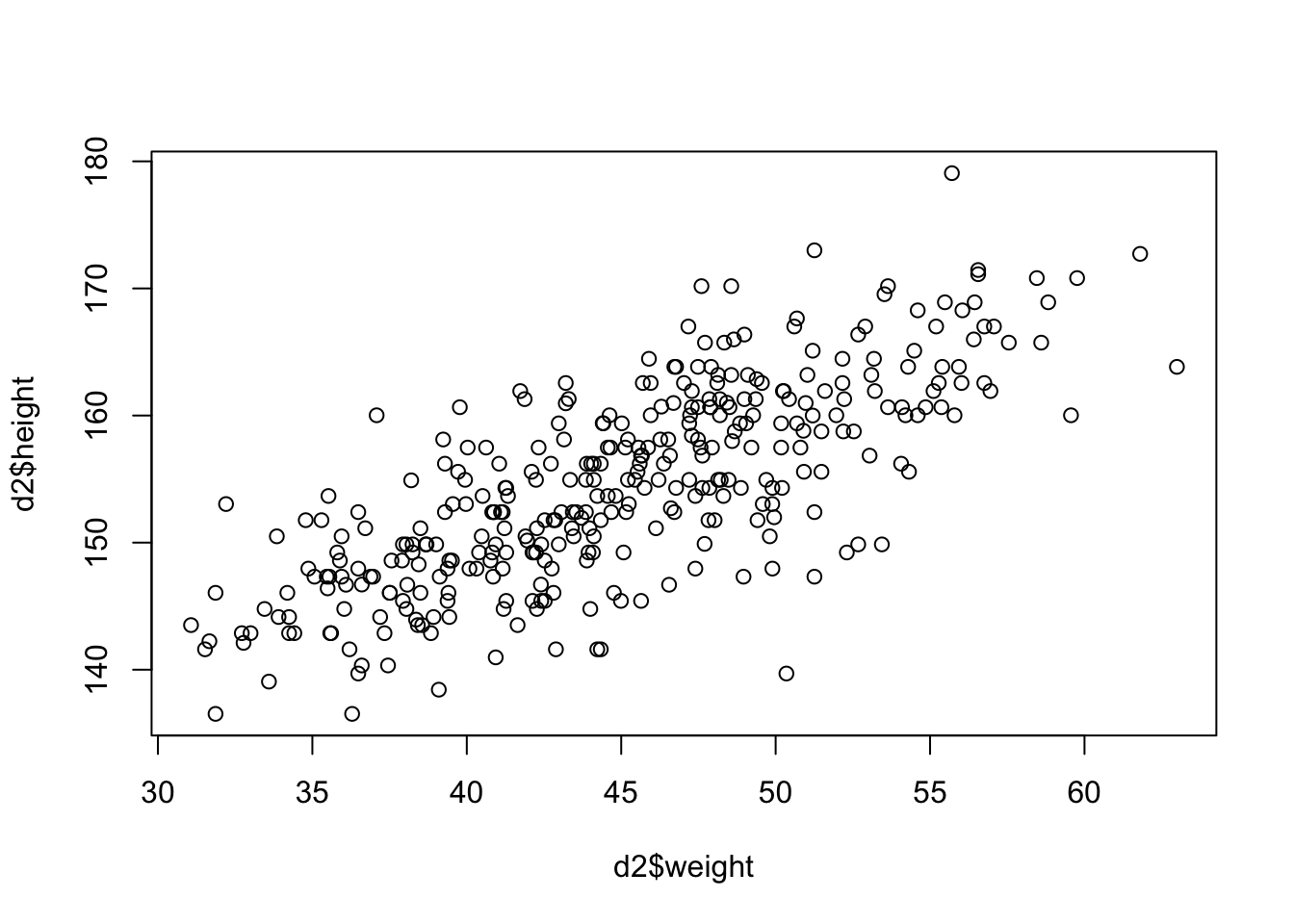
It’s not often that you see such a clean plot. The scatterplot indicates a linear relationship between the two variables. The higher the weight, the higher the height; with some deviations of course and we decide that normally distributed errors are a good idea. This relationsip is neither causal, nor deterministic.
- It is not causal since an increase in weight does not necessarily lead to an increase in height, especially in grown-ups.
- It is not deterministic since there are deviations from the line. It if was deterministic, we would not need statistical modeling.
For simpler notation, we will call d2$weight \(x\). \(\bar{x}\)
is the mean of \(x\).
3.1.1 Model definition
Let’s write down our model (again with the Swiss population prior mean):
\[\begin{eqnarray*} h_i &\sim& \text{Normal}(\mu_i, \sigma)\\ \mu_i &\sim& \alpha + \beta (x_i - \bar{x})\\ \alpha &\sim& \text{Normal}(171.1, 20)\\ \beta &\sim& \text{Normal}(0, 10)\\ \sigma &\sim& \text{Uniform}(0, 50) \end{eqnarray*}\]
Visualization of the model structure:
There are now additional lines for the priors of \(\alpha\) and \(\beta\) (compared to the simple mean model before). The model structure also shows the way to simulate from the prior. One starts at the top and ends up with the heights.
- \(h_i\) is the height of the \(i\)-th person and we assume it is normally distributed.
- \(\mu_i\) is the mean of the height of the \(i\)-th person and we assume it is linearly dependent on the difference \(x_i-\bar{x}\). Compared to the intercept model, a different mean is assumed for each person depending on his/her weight.
- \(\alpha\) is the intercept and we use the same prior as before.
- \(\beta\) is the slope of the line and we use the normal distribution as prior for it, hence it can be positive or negative and how plausible each value is, is determined by that specific normal distribution. Note, that we could easily adapt the distribution to any distribution we like.
- The prior for \(\sigma\) is unchanged.
- \(x_i - \bar{x}\) is the deviation of the weight from the mean weight, thereby we center the weight variable. This is a common practice in regression analysis. A value \(x_i - \bar{x} > 0\) implies that the person is heavier than the average.
The linear model is quite popular in applied statistics and one reason is probably the rather straightforward interpretation of the coefficients: A one unit increase in weight is on average (in the mean) associated with a \(\beta\) unit increase/decrease (depending if \(\beta\) is \(>0\) or \(<0\)) in height.
3.1.2 Priors
We want to plot our prior predictions to get a feeling what the model would predict without seeing the data. This is a kind of “sanity check” to see if the priors and the model definition are reasonable. Again, we just draw from the assumed distributions for \(\alpha\) and \(\beta\) 100 times and draw the corresponding lines. Just as the model definition says.
set.seed(2971)
N <- 100 # 100 lines
a <- rnorm(N, 171.1, 20)
b <- rnorm(N, 0, 10)
xbar <- mean(d2$weight)
# start with empty plot
plot(NULL, xlim = range(d2$weight), ylim = c(-100, 400),
xlab = "weight", ylab = "height")
abline(h = 0, lty = 2) # horizontal line at 0
abline(h = 272, lty = 1, lwd = 0.5) # horizontal line at 272
mtext("b ~ dnorm(0, 10)")
# Overlay the 100 lines
for (i in 1:N) {
curve(a[i] + b[i] * (x - xbar),
from = min(d2$weight), to = max(d2$weight),
add = TRUE, col = col.alpha("black", 0.2))
}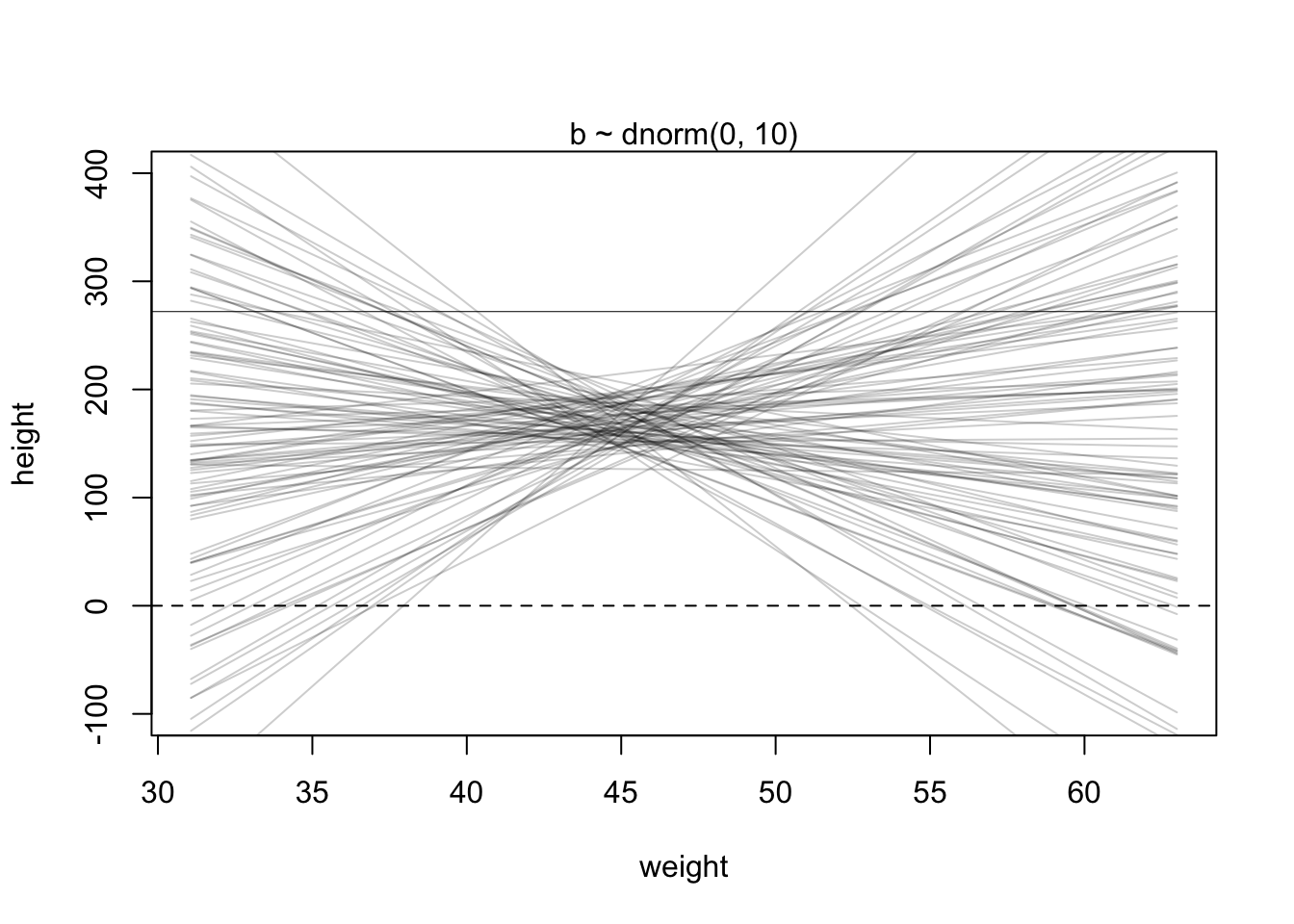
This linear relationship defined with the chosen priors seems rather non-restrictive. According to our priors, one could see very steeply rising or falling relationships between weight and expected heights. We could at least make the priors for the slope (\(\beta\)) non-negative. One possibility to do this is to use a log-normal distribution for the prior of \(\beta\) which can only take non-negative values.
\[\beta \sim \text{Log-Normal}(0, 1)\]
Lets plot the priors again.
set.seed(2971)
N <- 100 # 100 lines
a <- rnorm(N, 171.1, 20)
b <- rlnorm(N, 0, 1)
xbar <- mean(d2$weight)
plot(NULL, xlim = range(d2$weight), ylim = c(-100, 400),
xlab = "weight", ylab = "height")
abline(h = 0, lty = 2) # horizontal line at 0
abline(h = 272, lty = 1, lwd = 0.5) # horizontal line at 272
mtext("b ~ dlnorm(0, 1)")
# Overlay the 100 lines
for (i in 1:N) {
curve(a[i] + b[i] * (x - xbar),
from = min(d2$weight), to = max(d2$weight),
add = TRUE, col = col.alpha("black", 0.2))
}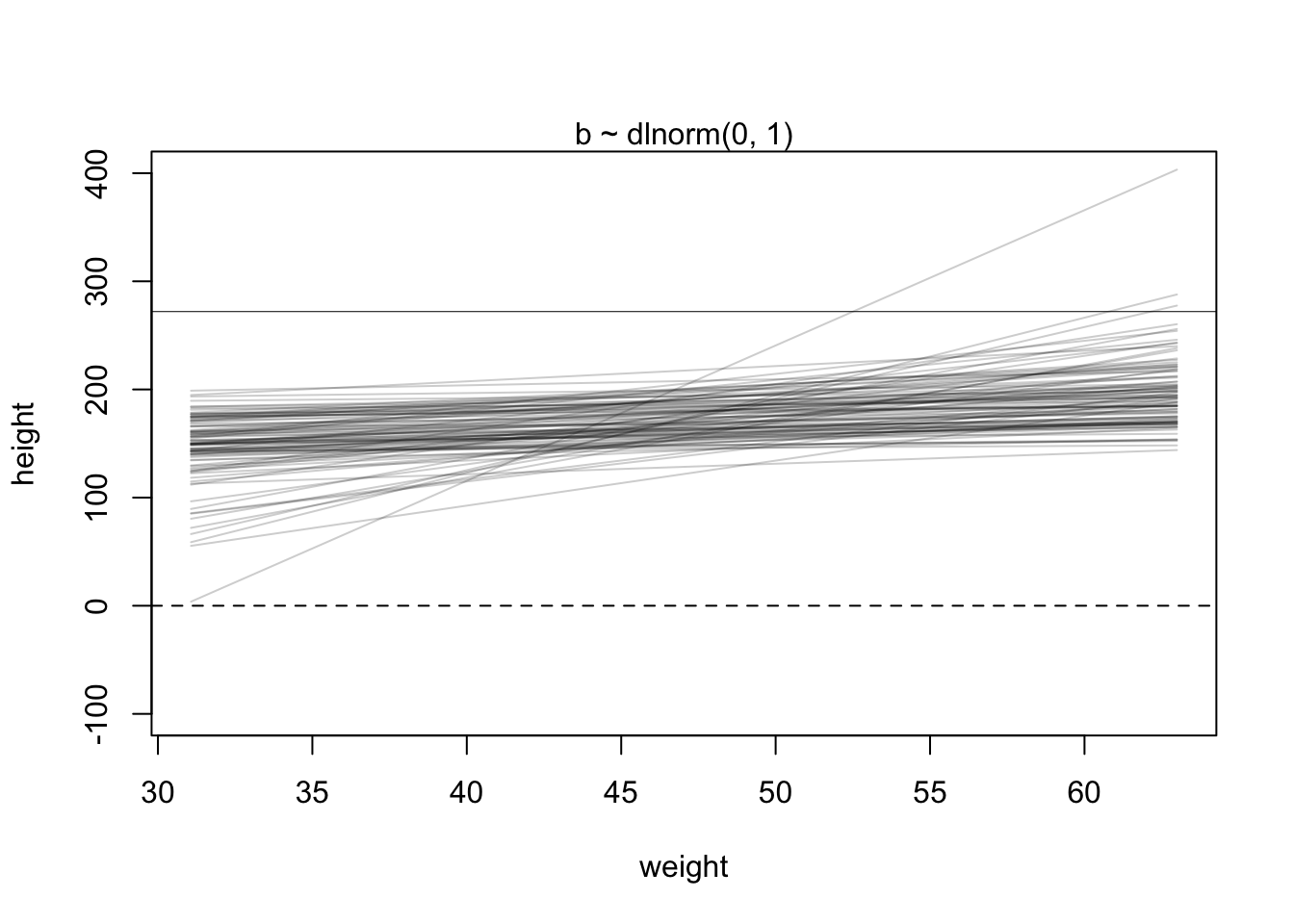
This seems definitely more realistic. There is some sort of positive linear relationship between weight and expected height.
3.1.3 Fit model
Now, let’s estimate the posterior/fit the model as before:
# load data again, since it's a long way back
library(rethinking)
data(Howell1)
d <- Howell1
d2 <- d[d$age >= 18, ]
xbar <- mean(d2$weight)
# fit model
mod <- quap(
alist(
height ~ dnorm(mu, sigma),
mu <- a + b * (weight - xbar),
a ~ dnorm(171.1, 20),
b ~ dlnorm(0, 1),
sigma ~ dunif(0, 50)
) ,
data = d2)Note that the model definition was now directly included in the quap function.
Let’s look at the marginal distributions of the parameters:
## mean sd 5.5% 94.5%
## a 154.6001022 0.27030753 154.1680986 155.0321059
## b 0.9032812 0.04192363 0.8362791 0.9702832
## sigma 5.0718802 0.19115470 4.7663781 5.3773824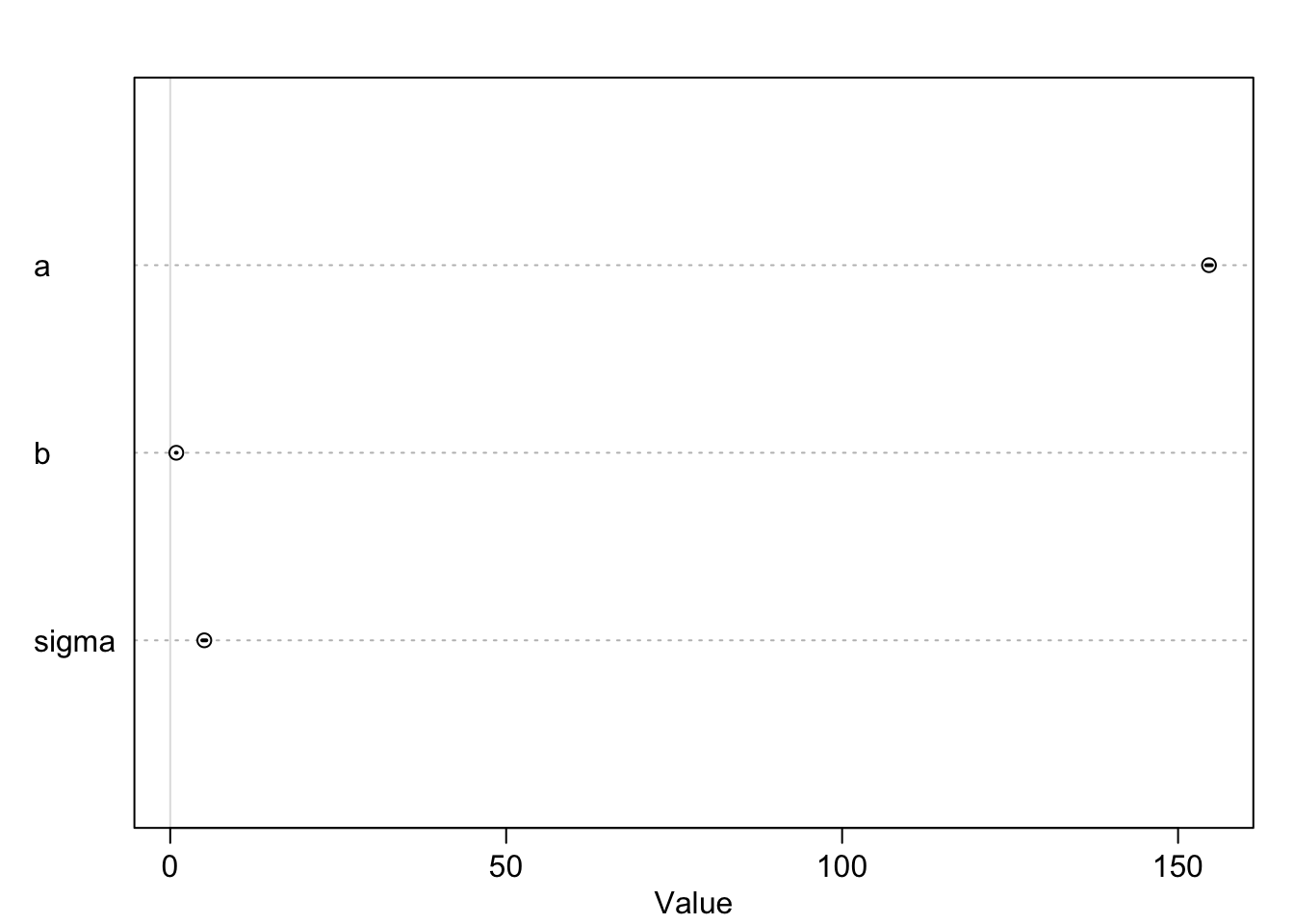
Note, that the credible intervals in the plot of the coefficients are hardly noticable. The reason is that the intercept \(a\) is rather large, whereas \(b\) and sigma are comparativly small. The plot is scaled to the largest parameter.
We can improve this by centering the height variable as well. Or, we could standardize both weight and height. This would change the interpretation of the \(\beta\) parameter. It would then be the expected change in standard deviations when changing weight by one standard deviation. See exercise 12.
The analysis yields estimates for all our parameters of the model: \(\alpha\), \(\beta\) and \(\sigma\). The estimates are the mean of the posterior distribution.
See exercise 2.
Interpretation of \(\beta\): The mean of the posterior distribution of \(\beta\) is 0.9. A person with a weight of 1 kg more weight can be expected to be 0.9 cm taller. A 89% credible interval for this estimate is \([0.83, 0.97]\). We can be quite sure that the slope is positive (of course we designed it that way too via the prior).
It might also be interesting to inspect the variance-covariance matrix, respectively the correlation between the parameters as we did before in the intercept model. Remember, these are the correlations of parameters in the multivariate (because three paremeters simulatenously) posterior distribution.
## a b sigma
## 0.07306616 0.00175759 0.03654012## a b sigma
## a 1 0 0
## b 0 1 0
## sigma 0 0 1diag(vcov(mod))gives the variances of the parameters andcov2cor(vcov(mod))the correlations. As we can see the correlations are (near) zero. Compare to the graphical display of the model structure. There is no connection.
3.1.4 Result
Graphical end result of fitting the model: We plot the marginal posterior distributions of \(\alpha\) and \(\beta\), and also the raw data with the found regression line.
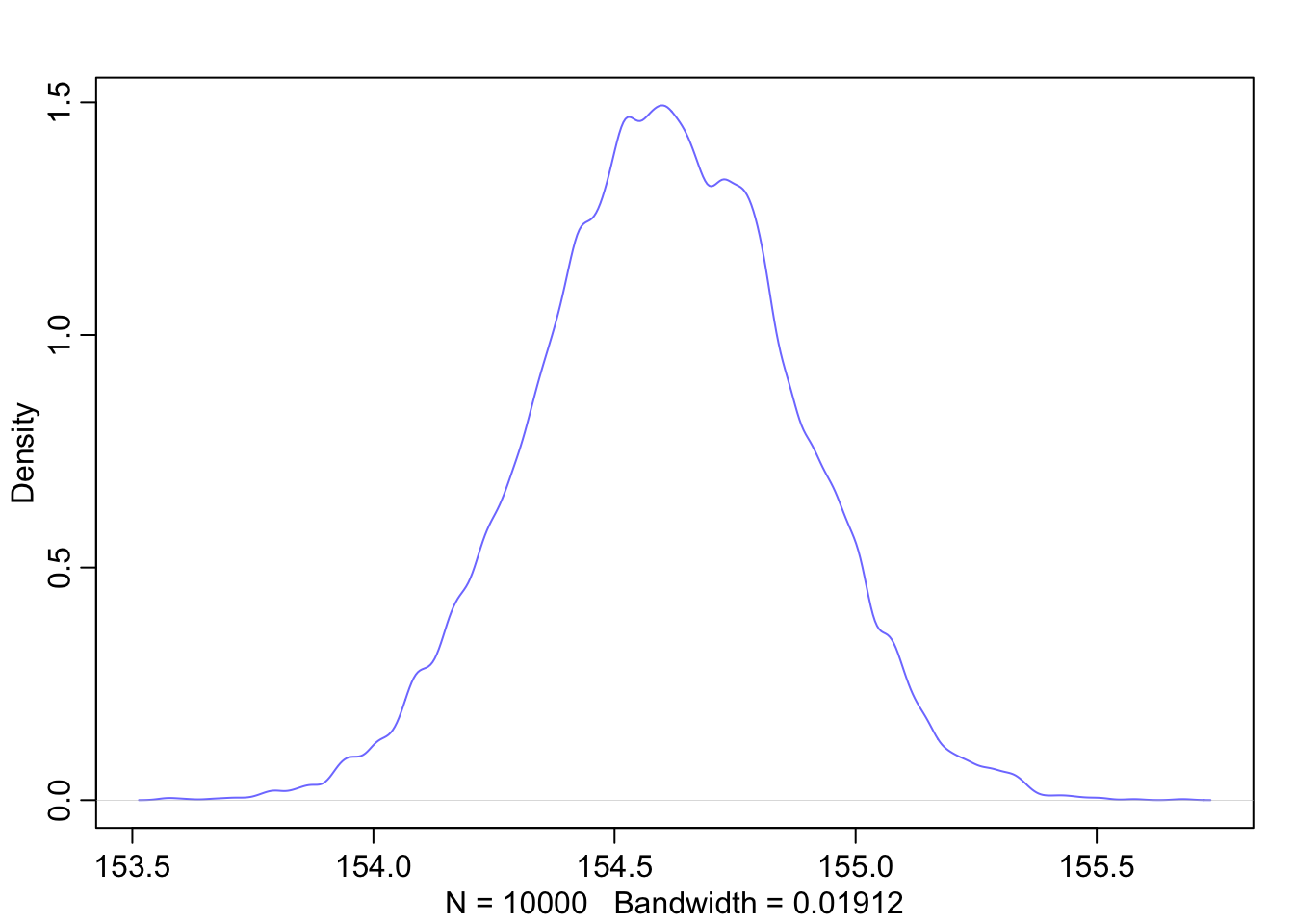
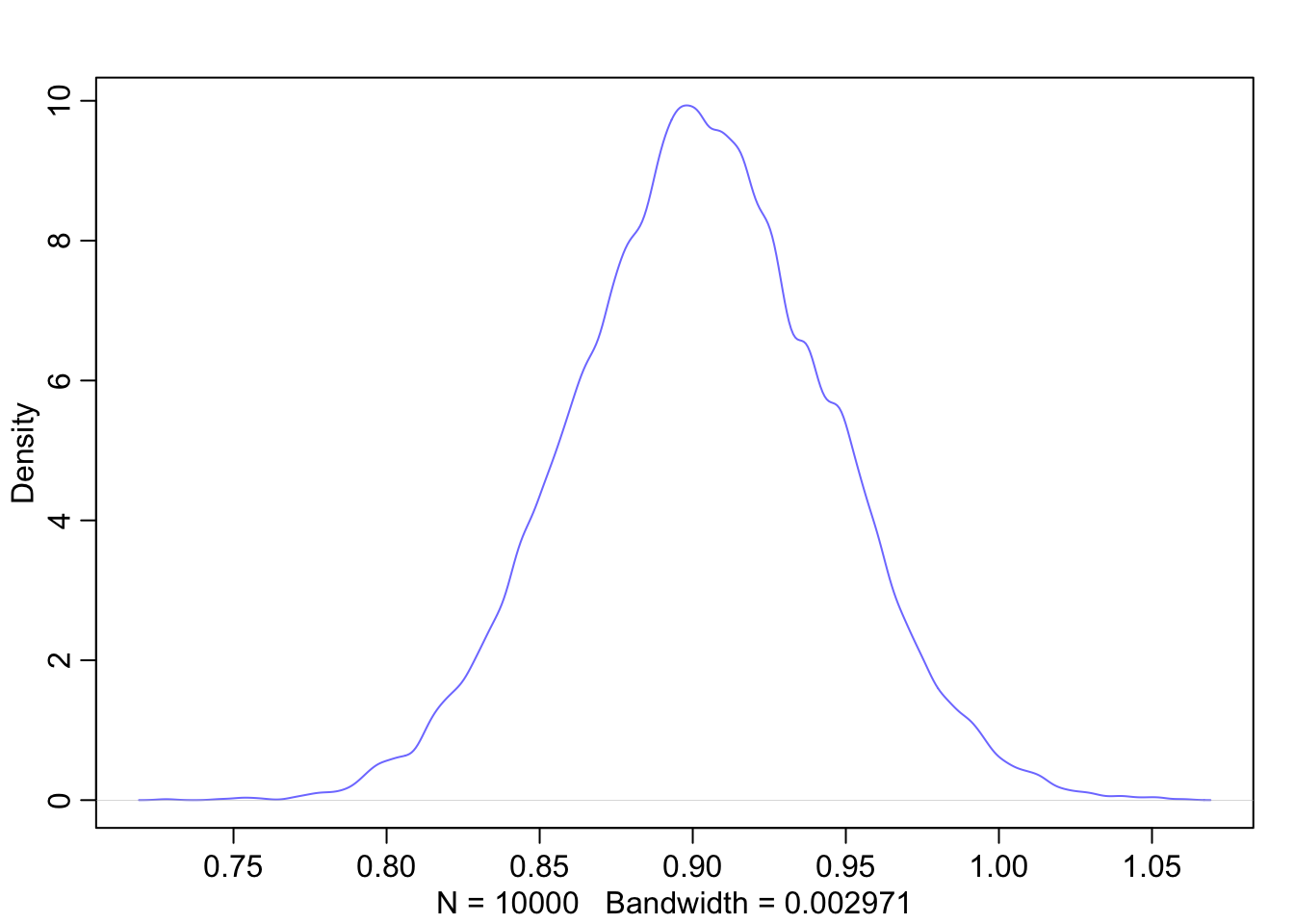
# both posteror plots seem symmetric
# we use the mean as point estimate
# for a and b.
a_quap <- mean(post$a)
b_quap <- mean(post$b)
plot(d2$height ~ d2$weight, col = rangi2)
curve(a_quap + b_quap * (x - xbar), add = TRUE)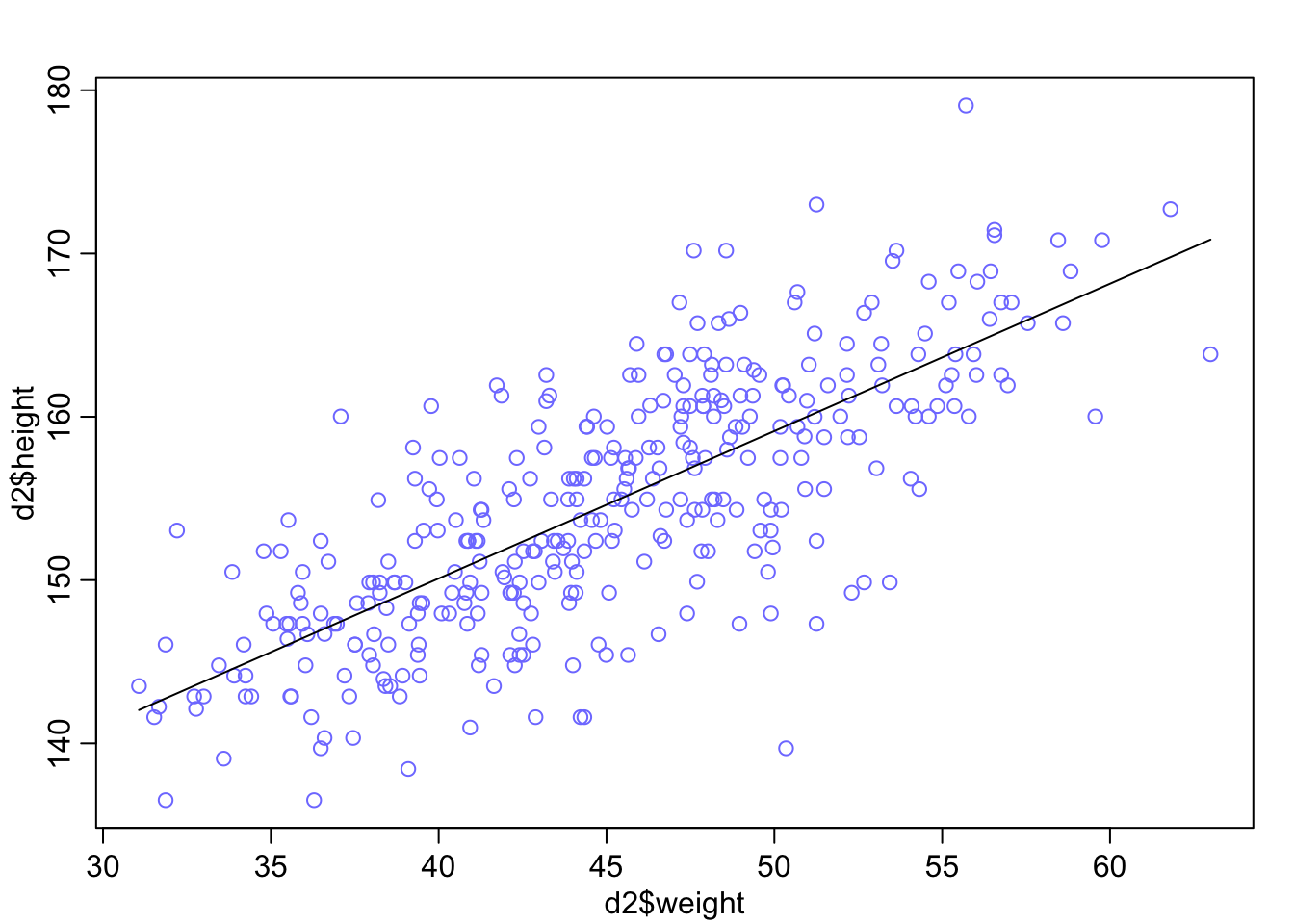
3.1.5 Credible bands
We could draw again and again from the posterior distribution
and calculate the means like above. Plotting the regression lines
with the respective parameters \(\alpha\), \(\beta\) would indicate
the variability of the estimates.
Note that we do not draw from the data (as one does in bootstrap resampling),
but from the posterior distribution.
The link function does this for us. It takes the posterior distribution we
have just fit, samples \(\alpha\) and \(\beta\) from it, calculates the mean and then
samples from this normal distribution for the mean at a given weight.
Refer to pages 98-106 in the current version of the book Statistical Rethinking
for all details.
# Define a sequence of weights for predictions
weight.seq <- seq(from = 25, to = 70, by = 1)
# Use the model to compute mu for each weight
mu <- link(mod, data = data.frame(weight = weight.seq))
str(mu)## num [1:1000, 1:46] 138 136 137 136 137 ...# Visualize the distribution of mu values
plot(height ~ weight, d2, type = "n") # Hide raw data with type = "n"
# Loop over samples and plot each mu value
for (i in 1:100) {
points(weight.seq, mu[i, ], pch = 16, col = col.alpha(rangi2, 0.1))
}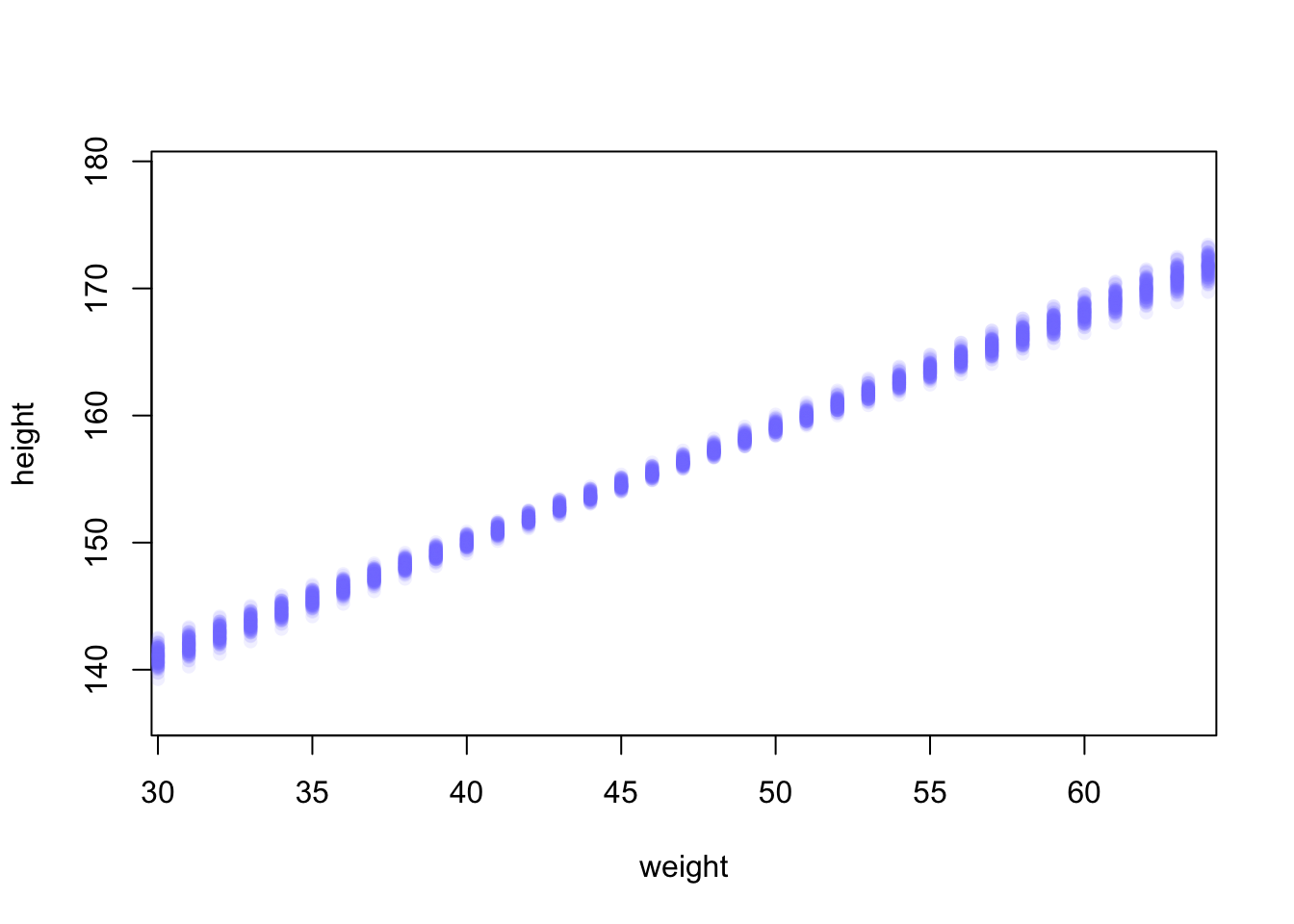
The link function fixes the weight at the values in weight.seq and
draws samples from the posterior distribution of the parameters. Above,
the first \(100\) (of \(1000\)) rows are used.
We can also draw a nice shade (using all 1000 rows of the \(\mu\)-matrix) for the regression line:
# Summarize the distribution of mu
mu.mean <- apply(mu, 2, mean)
mu.PI <- apply(mu, 2, PI, prob = 0.89)
plot(height ~ weight, d2, col = col.alpha(rangi2, 0.5))
lines(weight.seq, mu.mean)
shade(mu.PI, weight.seq)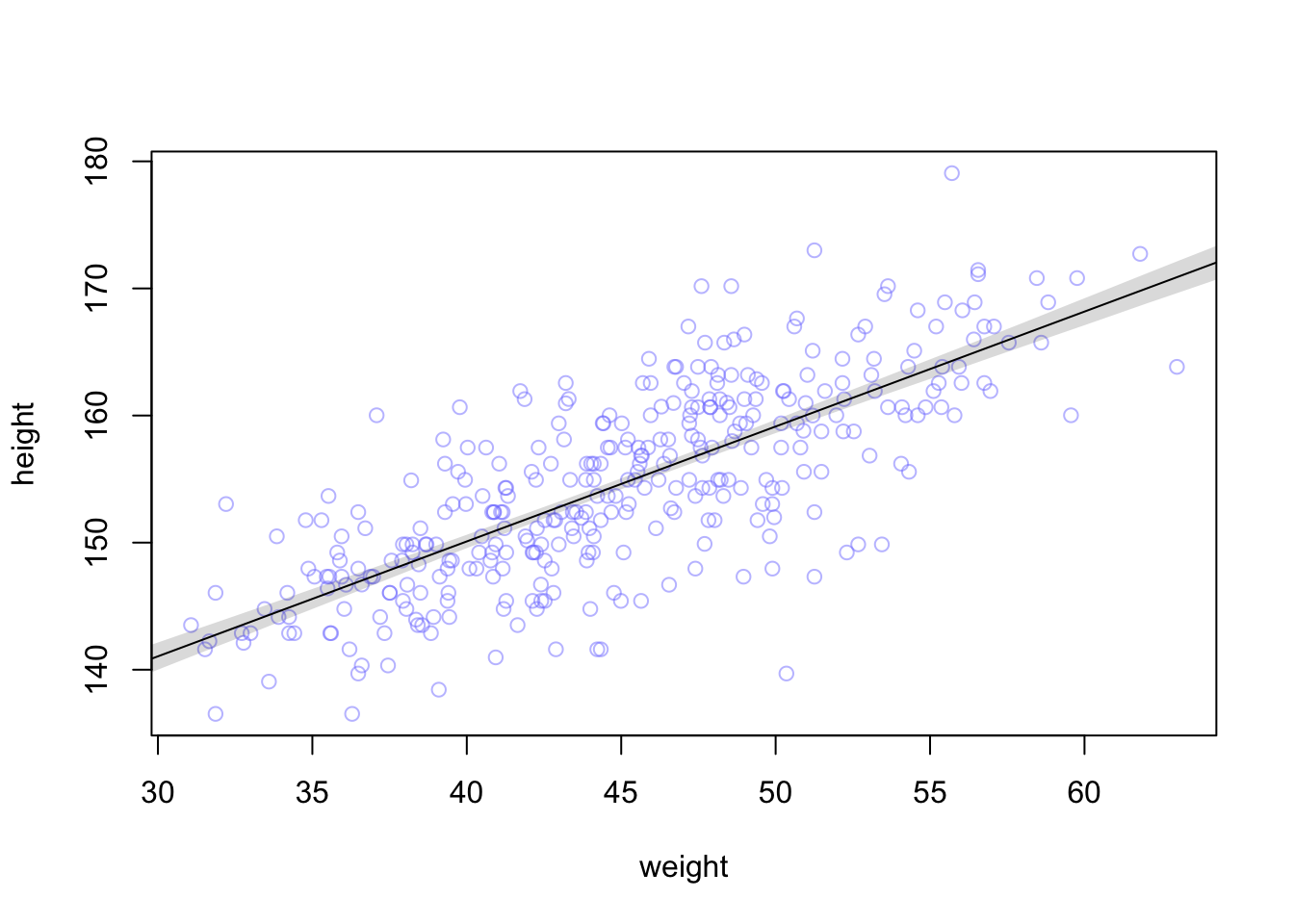
The function PI from the rethinking package calculates the 89% percentile interval
for the mean of the height at a certain weight. The apply function
apples this function to each columns (hence the 2) of the matrix mu.
As we can see, we are pretty sure about the mean of height which we wanted to model in the first place.
Mean modeling is one thing, individual prediction is another. Given a certain weight of a person, what is the height of the same person? The first line in the model definition (\(height_i \sim Normal(\mu_i, \sigma)\)) tells us that a person’s height is distributed around the mean (which linearly depends on weight) and is not necessary the mean itself.
To get to an individual prediction, we need to consider the uncertainty
of the parameter estimation and the uncertainty from the Gaussian distribution
around the mean (at a certain weight). We do this with sim.
# Simulate heights from the posterior
sim.height <- sim(mod, data = list(weight = weight.seq))
str(sim.height)## num [1:1000, 1:46] 138 130 130 147 136 ...# Compute the 89% prediction interval for simulated heights
height.PI <- apply(sim.height, 2, PI, prob = 0.89)
# Plot the raw data
plot(height ~ weight, d2, col = col.alpha(rangi2, 0.5))
# Draw MAP (mean a posteriori) line
lines(weight.seq, mu.mean)
# Draw HPDI (highest posterior density interval) region for mu
shade(mu.PI, weight.seq)
# Draw PI (prediction interval) region for simulated heights
shade(height.PI, weight.seq)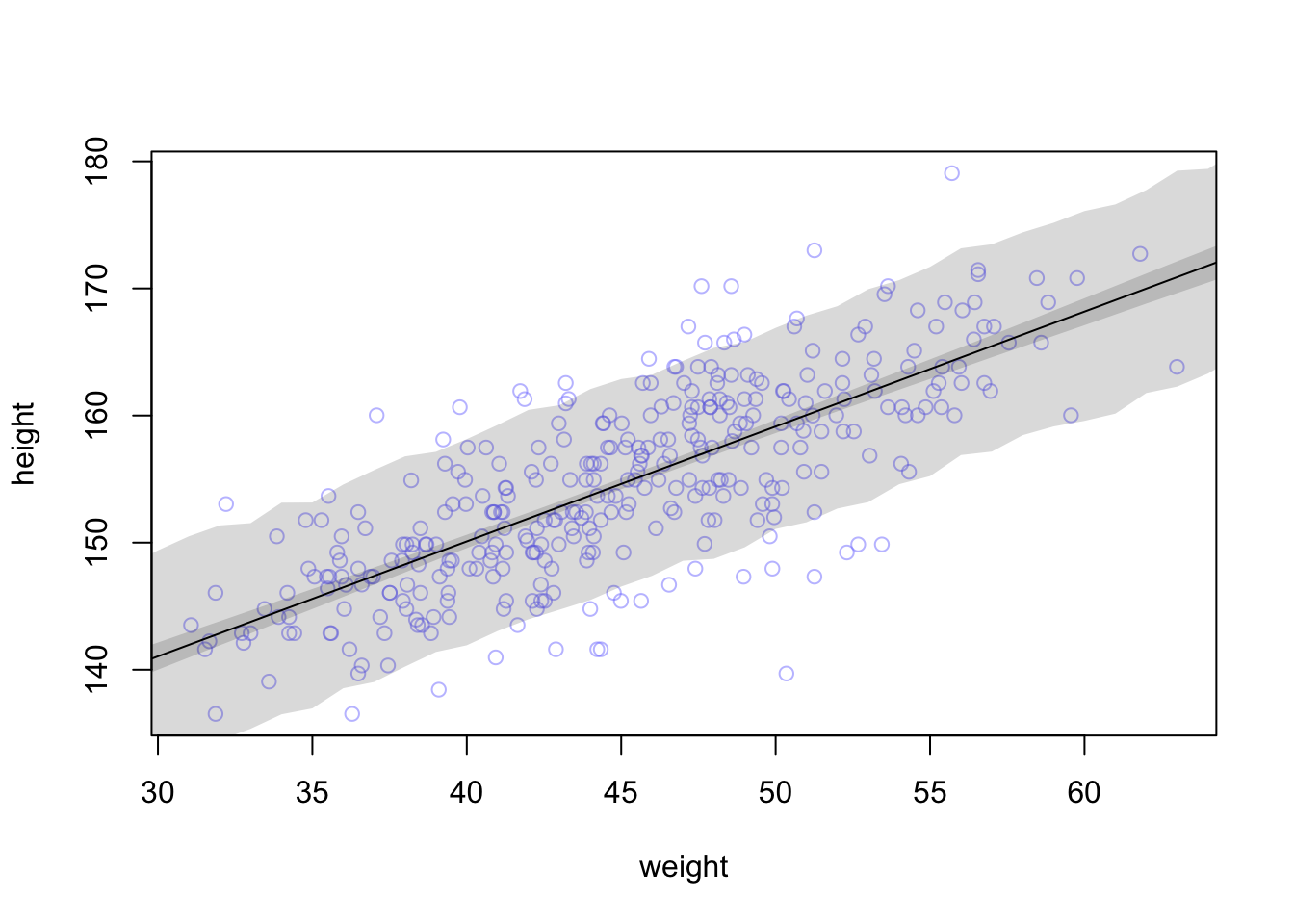
Here, the PI function is applied to the simulated heights and calculates the 89%
percentile interval for each weight.
The lighter and wider shaded region is where the model expects to find 89% of the heights of a person with a certain weight.
This part is sometimes a bit desillusioning when seen for the first time: Draw a horizontal line at 150 cm and see how many weights (according to the individual prediction) are compatible with this height. Weights from 30 to 50 kg are compatible with this height according to the 89% prediction interval:
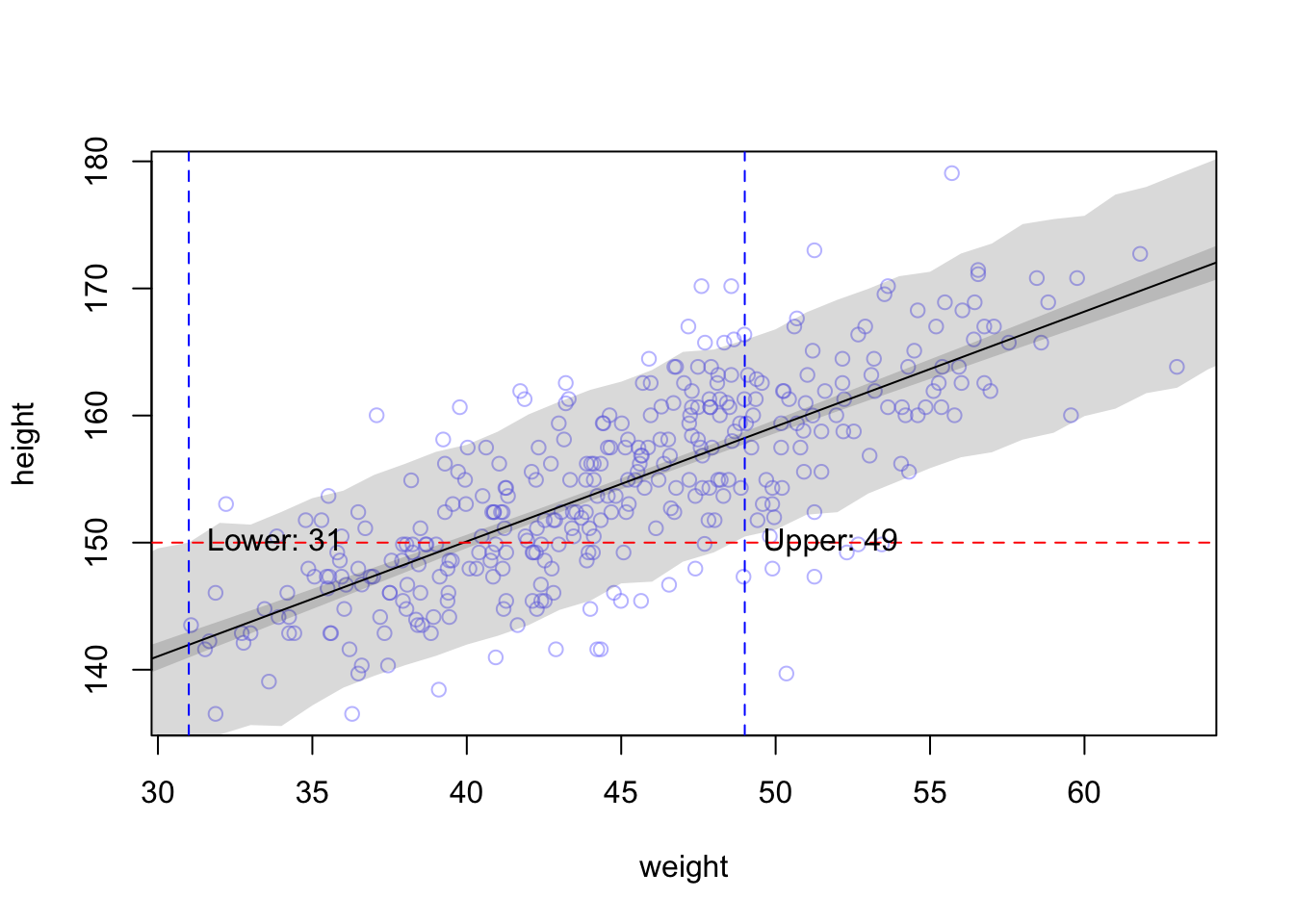
The higher the credibility, the wider the interval, the wider the range of compatible weights. In our example, more than 60% of the weight-range are plausible to predict a height of 150 cm.
## [1] 0.6265362On the other hand: We did not model the relationship this way. We modeled height depending on weight and not the other way around. In the next chapter, we will regress weight on height (yes, this is the correct order) and see what changes.
3.1.6 Summary
- We have added a covariate (weight) to the simple mean model to predict height.
- We have centered the weight variable.
- We have defined and refined priors for the intercept and slope.
- We have estimated the posterior distribution of the parameters using quadratic approximation with
quap. - We have visualized the result.
- We have created credible bands for mean and individual predictions.
3.2 Simple Linear Regression in the Frequentist Framework
We will now do the same analysis in the Frequentist framework while introducing some foundational theory along the way. I recommend reading the first couple of chapters from Westfall.
3.2.1 Model definition
Our linear model is defined as:
\[h_i = \beta_0 + \beta_1 x_i + \varepsilon_i\]
where
- \(\varepsilon_i\) is the error term with \(\varepsilon_i \sim N(0, \sigma^2), \forall i\)
- \(\beta_0\) is the unknown but fixed intercept
- \(\beta_1\) is the unknown but fixed slope
3.2.1.1 Model Assumptions of the Classical Regression Model (Westfall, 1.7):
The first and most important assumption is that the data are produced
probabilistically, which is specifically stated as
\[Y|X = x \sim p(y|x)\]
What does this mean?
- \(Y|X = x\) is the random variable Y conditional on X being equal to x, i.e. the distribution of \(Y\) if we know the value of \(X\) (in our example the weight in kg). This is a nice image of what is meant here.
- \(p(y|x)\) is the distribution of potentially observable \(Y\) given \(X = x\). In our case above this was the normal distribution with mean \(\mu_i\) and variance \(\sigma\).
You can play with this shiny app to improve your understanding. It offers the option “Bedingte Verteilung anzeigen”.
One always thinks about the so-called data generating process (Westfall, 1.2). How did the data come about? There is a process behind it and this process is attempted to be modeled.
Further assumptions:
Correct functional specification: The conditional mean function \(f(x) = \mathbb{E}(Y|X=x)\). In the case of the linear model, the assumption is \(\mathbb{E}(Y|X=x) = \alpha + \beta x\). The expectation of \(Y\) (height) depends linearly on \(x\) (weight). This assumption is violated when the true relationship is not linear or the data at least suggest that it is not linear, like here.
The errors are homoscedastic (constant variance \(\sigma^2\)). This means the variances of all conditional distributions \(p(y|x)\) are constant (\(=\sigma^2\)). This assumption is (for instance) violated if points are spreading out more and more around the regression line, indicating that the errors are getting larger.
Normality. For the classical linear regression model all the conditional distributions \(p(y|x)\) are normal distributions. It could well be, that the errors are not nicely normally distributed around the regression line, for instance if we have a lot of outliers upwards and the distribution is skewed, like here (Figure 5.20).
The errors are independent of each other. The potentially observable \(\varepsilon_i = Y_i - f(\mathbf{x_i}, \mathbf{\beta})\) is uncorrelated with \(\varepsilon_j = Y_j - f(\mathbf{x_j}, \mathbf{\beta})\) for \(i \neq j\). This assumption is violated if the errors are correlated, here is an example: The true data comes from a sine curve and we estimate a linear model (green), which does not fit the data well (left plot). The residuals plot shows clear patterns (right plot) and indicates that the errors are correlated. Specifically, the errors around \(x=2\) and \(x=4\) are negatively correlated (see exercise 6).
##
## Attaching package: 'patchwork'## The following object is masked from 'package:MASS':
##
## area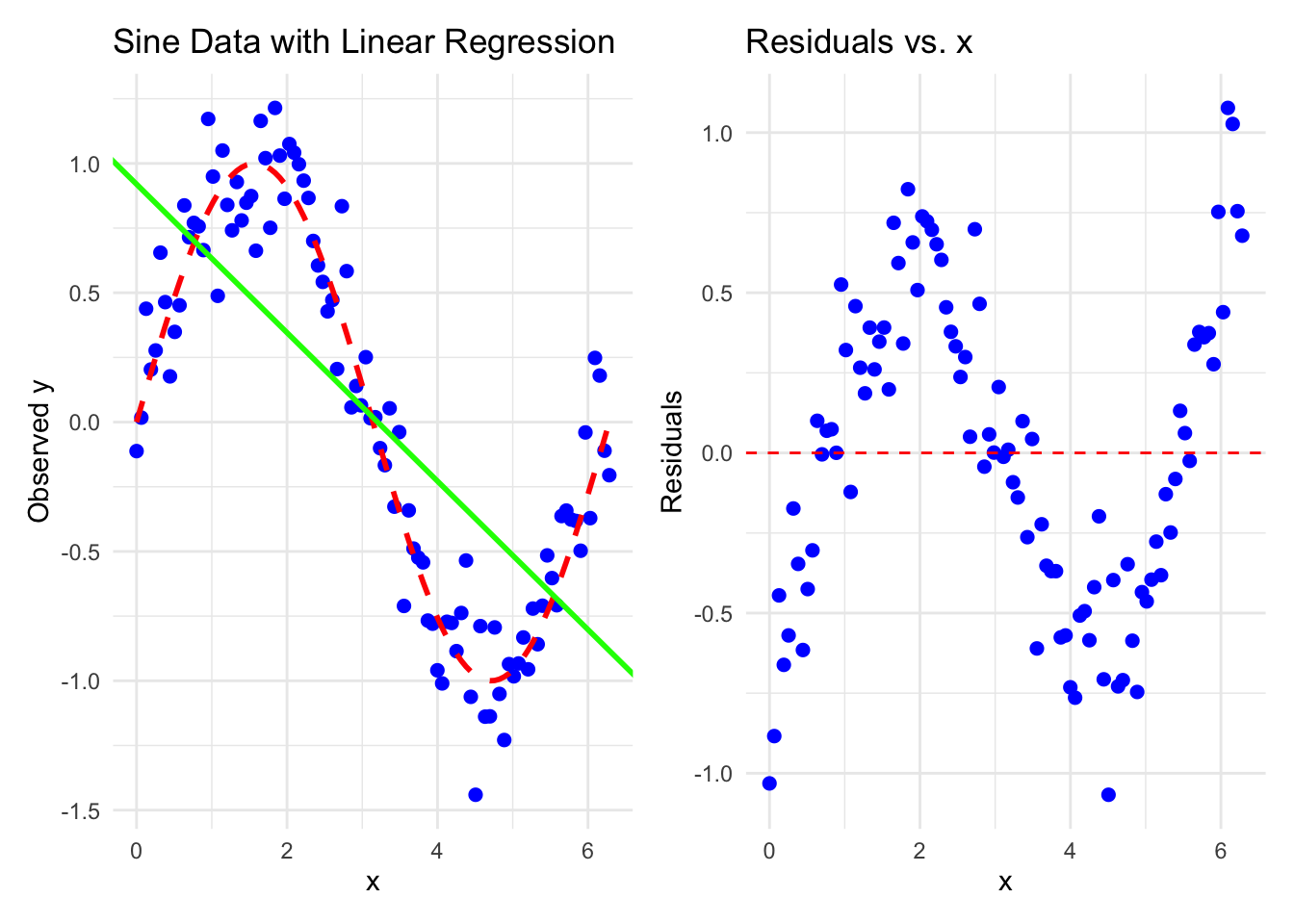
In the case above, the errors are not conditionally independent. If we condition on \(X=2\) and \(X=4.5\), the errors are correlated (\(r \sim -0.3\)), which they should not be.
These assumptions become clearer as we go along and should be checked for every model we fit. They are not connected, they can all be true or false. The question is not “Are the assumptions met?” since they never are exactly met. The question is how “badly” the assumptions are violated?
Remember, all models are wrong, but some are useful.
In full, the classical linear regression model can be written as:
\[Y_i|X_i = x_i \sim_{independent} N(\beta_0 + \beta_1 x_{i1} + \dots \beta_k x_{ik},\sigma^2)\] for \(i = 1, \dots, n\).
Interpretation of this formula:
The outcome variables \(Y_i\) are independently (from each other, since the errors are indepentent from each other) conditionally normally distributed (conditioned on \(X_i=x_i\)) with a mean that is linearly depending on true but unknown parameters \(\beta_0, \beta_1, \dots, \beta_k\) and a constant variance \(\sigma^2\).
3.2.2 Fit the model
Again, we fit the model using the least squares method. For a neat animated explanation, visit this video. There are literally hundreds of videos on the topic. Choose wisely. Not all are good. If in doubt, use our recommended books as reading materials. This is the most reliable source. A hint along the way: Be very sceptical if you ask GPT about information, although for this special case one has a good chance of getting a decent answer due to the vast amount of training data.
One has to minimize the sum of squared differences between the true heights and the model-predicted heights in order to find \(\beta_0\) and \(\beta_1\).
\[SSE(\beta_0, \beta_1) = \sum_{i=1}^n (y_i - (\beta_0 + \beta_1 x_i))^2\]
We omit the technical details (set derivative to zero and solve the system) and give the results for \(\beta_0\) and \(\beta_1\):
\[ \hat{\beta_0} = \bar{y} - \hat{\beta_1} \bar{x}, \] \[ \hat{\beta_1} = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} = \frac{s_{x,y}}{s_x^2} = r_{xy} \frac{s_y}{s_x}. \]
where:
- \(r_{xy}\) is the sample correlation coefficient between \(x\) and \(y\)
- \(s_x\) and \(s_y\) are the uncorrected sample standard deviations of \(x\) and \(y\)
- \(s_x^2\) and \(s_{xy}\) are the sample variance and sample covariance, respectively
Interpretation of \(\hat{\beta}_0\) and \(\hat{\beta}_1\): see exercise 3.
Let’s use R again to solve the problem:
library(rethinking)
data(Howell1)
d <- Howell1
d2 <- d[d$age >= 18, ]
mod <- lm(height ~ weight, data = d2)
summary(mod)##
## Call:
## lm(formula = height ~ weight, data = d2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.7464 -2.8835 0.0222 3.1424 14.7744
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 113.87939 1.91107 59.59 <2e-16 ***
## weight 0.90503 0.04205 21.52 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.086 on 350 degrees of freedom
## Multiple R-squared: 0.5696, Adjusted R-squared: 0.5684
## F-statistic: 463.3 on 1 and 350 DF, p-value: < 2.2e-16Interpretation of R-output:
Call: The model that was fitted.Residuals: \(r_i = height_i - \widehat{height}_i\). Differences between true heights and model-predicted heights.Coefficients: Names for \(\beta_0\) and \(\beta_1\). We call them \(\hat{\beta}_0\) and \(\hat{\beta}_1\).Estimate: The (least squares) estimated value of the coefficient.Std. Error: The standard error of the estimate. This is a measure of how precise the estimator for the coefficient is.t value: The value of the \(t\)-statistic for the (Wald-) hypothesis test \(H_0: \beta_i = 0\).Pr(>|t|): The \(p\)-value of the hypothesis test.
Residual standard error: The estimate of \(\sigma\) which is also a model parameter (as in the Bayesian framework).Multiple R-squared: The proportion of the variance explained by the model (we will explain this below).Adjusted R-squared: A corrected version of the \(R^2\) which takes into account the number of predictors in the model.F-statistic: The value of the \(F\)-statistic for the hypothesis test: \(H_0: \beta_1 = \beta_2 = \dots = \beta_k = 0\). Note, the alternative hypotheses to this test is that any of the \(\beta_i\) is not zero. If that is the case, the model explains more than the mean model with just \(\beta_0\).
We could also solve the least squares problem graphically: We want to find the
values of \(\beta_0\) and \(\beta_1\) that minimize the sum of squared differences
which can be plotted as 3D function. Since the function is a sum of squared terms,
we should expected a paraboloid form.
All we have to do is to ask R which of
the coordinates (\(\beta_0\), \(\beta_1\)) minimizes the sum of squared errors.
The result confirms
the results from the lm function. The dot in red marks the spot
(Code is in the git repository):
## Intercept beta_0: 113.8794## Slope beta_1: 0.9050291